Alvy Ray Smith. A Biography of the Pixel. The MIT Press, 2021. Contents
Полимеры и красный интернет
Сеть ARPANET, которую в конце 1960-х создало Минобороны США, могла бы быть не курицей (прототипом интернета), а всего лишь яйцом (или кто из них главнее?), если бы номенклатура не зарубила проект советского интернета, едва тот начал проклевываться. А ведь пишут, что и концепцию электронных денег в СССР обдумывали еще в 1960-е, и безбумажный документооборот, и даже программирование с использованием естественного языка — когда самих разработчиков сегодняшних продуктов, скорее всего, еще и в проекте не было.
О судьбе полимеров (зачеркнуто: красного интернета) можно прочесть в книге историка медиа Бенджамина Питерса, вышедшей пять лет назад. А в 2021 году все то же MIT Press издает книгу кофаундера Pixar Элви Рэя Смита «Биография пикселя», в которой немало страниц посвящено советскому ученому Владимиру Александровичу Котельникову, чья теорема отсчетов 1933 года сделала мир пикселей возможным.
Котельников прожил 96 лет (1908—2005) и биография его насыщена множеством событий (например, ему грозил ГУЛАГ, но за него вступилась жена Маленкова Валерия Голубцова; а с 1973-го по 1980-й Котельников был председателем Верховного Совета РСФСР).
Владимир Котельников предположительно в 1930-е и в 2003 году
В 1949 году эту же теорему параллельно доказал американский математик Клод Шеннон и, как пишет Смит, в западной литературе ее чаще называют теоремой Шеннона. Хотя сам математик, как сообщается, на первенство не претендовал.
«Шеннон был нашим новым героем, когда дело касалось всего цифрового. Он был тем парнем, который первым использовал слово „бит” в печати. <...> Но это всего лишь американская версия — здесь вступает в силу закон об эпонимии Стиглера: „Ни одно научное открытие не названо в честь первооткрывателя” (этот закон, кстати, открыл не Стиглер). Так что, <...> без колебаний — вся заслуга в этой истории принадлежит Котельникову. А в Японии — Исао Сомея. В Англии — сэру Эдмунду Уиттекеру. В Германии — Герберту Раабе. <...> Несмотря на путаницу с атрибуцией, факт остается фактом: великая идея <...> была впервые четко, ясно и обстоятельно изложена и доказана Котельниковым в 1933 году. Западным людям может быть трудно поверить, что такая фундаментальная идея родилась в худшие дни сталинской России. Во время холодной войны нас учили, что российская наука была если не фикцией, как биология Лысенко, то в лучшем случае посредственностью или просто пропагандой».
Есть только волны и волны волн
Но прежде чем говорить о теореме отсчетов Котельникова, следует отмотать на два века назад. Французский математик и физик Жан-Батист Фурье создал принципиальную возможность мыслить в интересующем нас направлении. Коротко говоря, Фурье сформулировал идею о том, что любой одномерный сигнал представляет собой регулярные волны. Музыка — это звуковые волны разной частоты и амплитуды, тона и громкости соответственно.
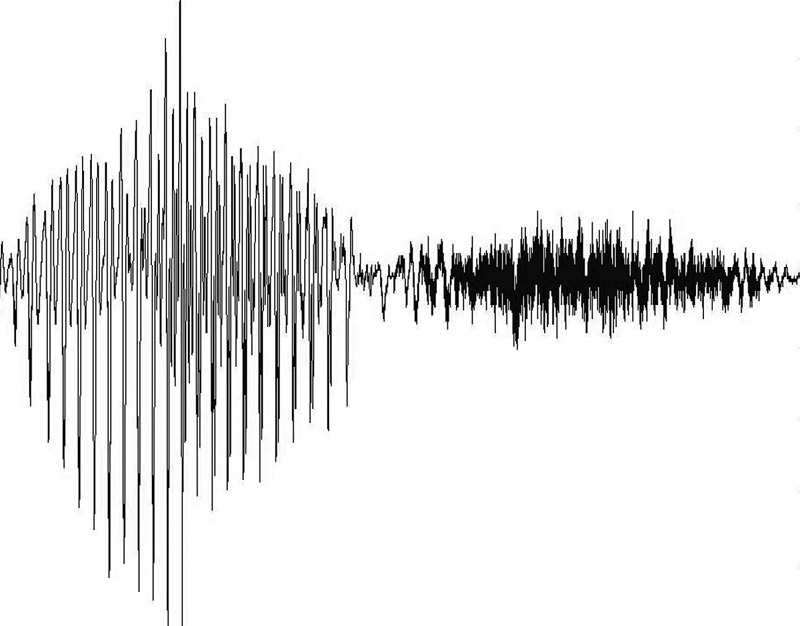Аудиосигнал. Источник: с. 20 книги
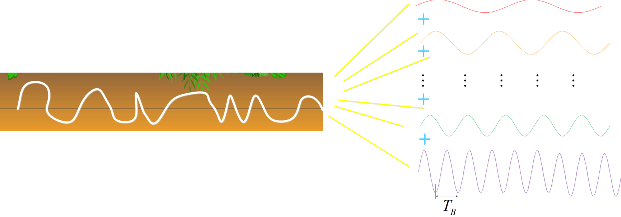
Фурье распространил это представление не только на звук, но и на все, что можно было бы назвать чувственным опытом. Все, что человек видит и слышит, — это тоже сумма волн, только двумерных.
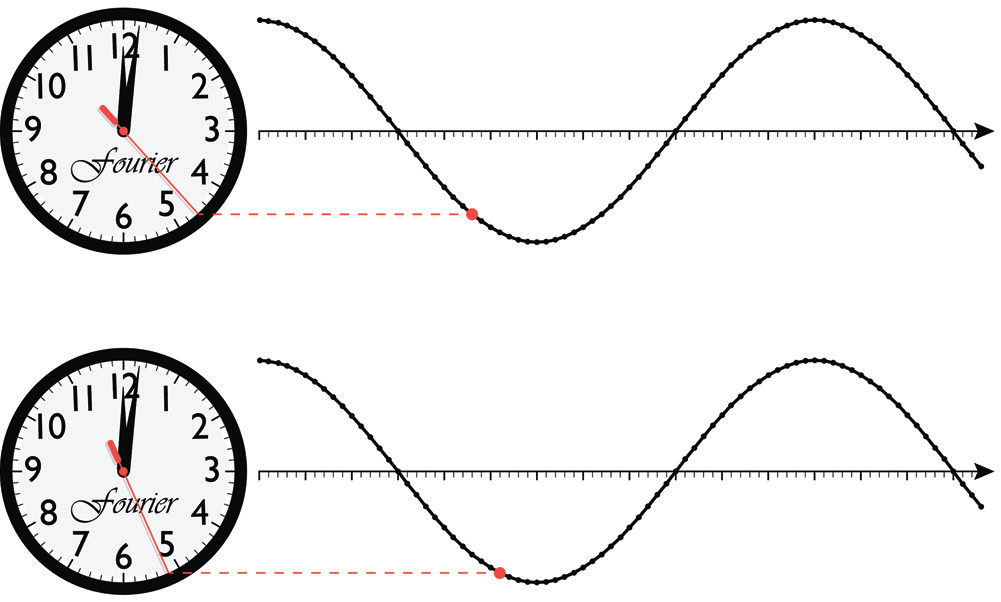Визуализация волны по аналогии с движением стрелки по циферблату. Источник: с. 16 книги
Одномерная волна — это размотанный (разомкнутый) круг (циферблат). Двумерная волна — размотанный цилиндр. Чтобы визуализировать волну в двух измерениях, представьте себе волну секундной стрелки часов, вытянутую перпендикулярно странице. Получается гофрированная поверхность, похожая на бороздчатое поле — как гофрированные пластиковые панели, которыми покрывают крыши и навесы. Или гофрированные чипсы.
«Посмотрите на край гофры — поперечное сечение — и увидите одномерную волну. <...> Основная идея Фурье состоит в том, что весь визуальный мир можно представить как сумму <...> гофрированных волн всех частот и амплитуд. <...> Борозды могут проходить с севера и юга, с востока на запад, с северо-востока на юго-запад или под любым другим углом и направлением».
Источник: с. 31 книги
Все визуальные паттерны, независимо от того, какими бы хаотичными они не казались, можно описать как комбинацию сумм регулярных волн Фурье. И в природе то же самое, хотя это и менее очевидно (за исключением океанских волн). Горные хребты. Травинки на лужайке или сами лужайки в лесу повторяются с предсказуемой частотой. Расстояние между листьями зависит от вида разных деревьев, но и здесь можно узреть волнообразную функцию. Расстояние между деревьями в лесу также имеет характерную частоту, зависящую опять же от вида деревьев.
Аналоговая бесконечность больше цифровой
Однако мы еще, кажется, не забыли, что собрались что-то рассказать о пикселях. Как говорил герой Довлатова: долго не кончать — преимущество мужчины, а не оратора.
Итак, что сделал Котельников со знанием, подаренным миром Фурье? Коротко: он определил, что у всякой волны есть, говоря грубее некуда, пиковые точки (отсчеты), которые позволяют убрать все моря, реки, горы, леса и поля с их неочевидными волнами — и никто ничего не заметит. Сейчас поясним, что это означает.
Элви Рэй Смит. Источник
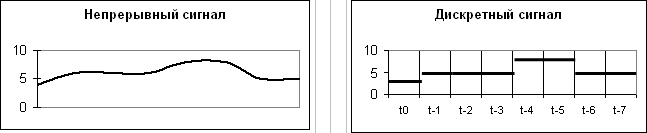
Большинство процессов в природе протекают непрерывно — например, меняется температура, давление или влажность воздуха, сила тока в проводнике, интенсивность света. Непрерывные процессы, функции и сигналы называются аналоговыми.
«Существует много разных видов бесконечности, но нам нужны только два — цифровая и аналоговая. <...> По мере того, как секундная стрелка перемещается по циферблату, можно вслед за ней попробовать сосчитать размеченные точки. Сколько их там? Вы можете начать считать: один, два, три и так далее, но вам придется делать это бесконечно. Это цифровая бесконечность. Всегда есть еще одно число. Математики называют ее счетной бесконечностью по очевидной причине. Другой вид бесконечности — аналоговой — не так прост. Рассмотрим две последовательные точки на волне. Сколько еще находится точек на волне между этими двумя точками? Ответ: их так много, что не сосчитать. Аналоговая бесконечность больше цифровой бесконечности, как бы странно это ни звучало. <...> Между любыми двумя точками на волне всегда есть еще одна точка».
Бесконечности обычно округляют до ближайших целых чисел — в результате получаются цифровые «сигналы» (в широком смысле). Цифровая шкала на столбике термометра фиксирует округленное значение температуры. Непрерывное время разбивается на секунды, минуты и часы. Во всех знаковых системах, созданных для сохранения и передачи информации, используется конечное число элементов.
Аналоговый сигнал и на конечном временном отрезке подразумевает бесконечное число значений. Но регистрирующие устройства фиксируют конечное число значений — так получаются дискретные сигналы (лат. discretus, «раздельный»). То есть здесь осуществляется перевод аналоговых непрерывных процессов, существующих в природе, в дискретные — цифровые.
Например, нам зачем-то понадобилось изучить движение змеи на песке. Если у нее все нормально с вестибулярным аппаратом, то траектория будет представлять собой предсказуемые зигзаги или, иначе говоря, гармоничные колебания одной маленькой волны в необъятном мире волн. Эти колебания можно описать синусоидальными функциями. А чтобы восстановить всю траекторию движения, нужно ориентироваться на колебания самой высокой частоты — на отсчеты Котельникова.
Если же траектория движения колеблется, то и в ней можно сыскать гармонию, поскольку она есть в любом сигнале (волне), что доказал еще Фурье.
Хрестоматийный Рабинович на вопрос, всегда ли он придерживался линии партии или колебался, отвечал, что колебался вместе с линией партии. Хрестоматийный Рабинович, конечно, флюгерист, но механику процесса интуитивно ухватил верно. Как всякий предмет можно разложить на атомы, так и сложную функцию (траекторию или звук) можно разложить на множество гармонических функций. И в каждом таком вираже хрестоматийный Рабинович будет гармоничен в своей «преданности».
Если вернуться к змее, то можно убрать и ее, и песок вместе с оставленным на ней следом — и если мы знаем высотные колебания (отчеты), мы можем восстановить ее путь на песке. То же самое и со звуком — убираем звуковой сигнал и восстанавливаем его по отсчетам.
«То есть можно выбросить вообще все — и при этом не потерять ничего. Вот по сути и вся магия открытия Котельникова. Если вы этому не удивились, то я в свое время — очень даже», — говорит Элви Рэй Смит.
Пиксель невозможно увидеть
Возвращаемся к чипсам и гофрированной кровле. Они, как мы уже сказали, представляют собой сумму 2D-волн. Какой же будет 3D-волна? Примерно такой.
А вот она в разрезе. Была волна трехмерная, стала двумерная. В поперечном сечении двумерной мы видим уже более-менее нам знакомую одномерную волну. Все сходится, спасибо товарищу председателю.
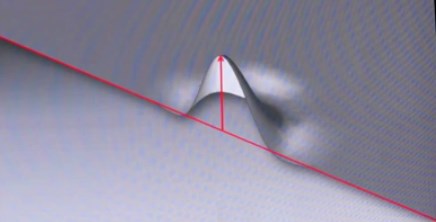
Источник: с. 57 книги
Можно было бы сказать, что именно так и выглядит пиксель. Если бы его можно было увидеть. Распространенное представление, что пиксель — это маленькие квадратики, на которые рассыпается сильно увеличенное изображение, неверно. Закреплению этой неправды способствует и слово «пикселизация», означающее описанный только что процесс. Маленькие горящие точки на дисплее, из которых собирается всякое изображение — это аналоговый свет, который, можно сказать, порождается функцией. Эти точки следовало бы называть элементами отображения, а не пикселями, отмечает Элви Рэй Смит.
Пиксель невозможно увидеть, потому что там буквально не на что смотреть. Но не в том смысле, в каком все тот же хрестоматийный Рабинович раздавал пустые листовки на Красной площади, а когда сотрудники КГБ спросили его, что означает такой перформанс, ответил: «А что писать? И так все понятно».
Нет, пиксель — это ничто, это точка с нулевым диаметром, у которой нет формы, протяженности и ширины. У пикселя есть только число, обозначающее оттенок серого (тут нет отсылки к семейной кинокартине Тейлора-Джонсона — в книге Элви Рэя Смита можно узнать подробнее, о чем именно идет речь). Или три числа — если элемент отображения цветной.
Но из такого строительного материала — из этого «ничто» — и состоит по сути цифровая вселенная.
Иллюстрация из книги Андрея Зарецкого и Александра Труханова. «Энциклопедия профессора Фортрана». М.: «Просвещение», 1991. Источник
Первые игры «младенца»
Еще немного цифровой археологии. В своих изысканиях Элви Рэй Смит пытался найти первые в истории человечества «пиксели» (в кавычках, потому что речь о зримых пикселях). И снова удивился, потому что ранее думал, что история компьютерной графики началась в 1960-е. Однако обнаружилось, что первый «пиксель» родился в 1948 года вместе с первым компьютером: Манчестерской малой экспериментальной машиной, которую еще называют «младенцем». Вес новорожденного — 27 тонн, рост — 7 метров, обхват талии — 15 метров. Вычислительная мощность — с ума сойти — 357 операций умножения в секунду (или 5 000 операций сложения — это попроще).
Где-то примерно в это же время создали первое цифровое изображение (в нижнем левом углу), в 1951 году в Манчестере — первую компьютерную игру (на коллаже внизу посередине), а в 1953-м уже в Кембридже — вторую (справа).
«Младенец» и его игры
Потом следуют более известные исторические вехи: 1963 год и начало компьютерной графики, ознаменованное созданием Айвеном Сазерлендом 2D-программы Sketchpad в Манчестерском технологическом институте. Следом Тимоти Джонсон написал программу Sketchpad III — и это по сути уже была 3D-графика.
Еще один умный человек — Гордон Мур, один из основателей Intel — в 1965 году вывел закономерность в темпах прогресса технологий — свой знаменитый закон Мура. Сегодня, когда говорят о новых чипах или росте возможностей компьютеров будущего, закон Мура упоминается как барьерная планка, которую следует преодолеть. По этому закону количество транзисторов, размещаемых на кристалле интегральной схемы, удваивается через определенные промежутки времени. В наше время предельная плотность размещения вентилей на кремниевой подложке давно уже достигнута и разработчики сосредоточились на распараллеливании процессов (например, увеличивая количество ядер).
Современный человек придумал, например, чип размером с коврик на 850 000 ядер. Противоположный пример миниатюризации — планирующий в воздухе будто семена клена чип в 1 мм — с антенной для беспроводной связи и датчиками, передающими данные на смартфон или компьютер. Залетит такой к кому-то в дом, никто и не заметит. И на той стороне узнают, что у хозяев на обед.
Или что-нибудь еще.