Дэвид Дарлинг, Агниджо Банерджи. Эта странная математика. На краю бесконечности и за ним. М.: АСТ; Corpus, 2021. Перевод с английского Алексея Глущенко. Содержание
Где выдают «окончательную бумажку»
«Математика — единственная наука, где возможна абсолютная достоверность. Ее утверждения и теоремы могут быть доказаны безусловно и безоговорочно и останутся истинными уже навсегда».
Всякая естественно-научная концепция — консенсус представителей научного сообщества, то есть не аксиоматика ни разу. Поэтому не исключено, что завтра концепция изменится, и если она не будет полностью опровергнута, то по меньшей мере мир узнает о ее неточности или неполноте (что время от времени и происходит).
А теореме Пифагора уже примерно 2 500 лет — и еще не родился тот человек, что опроверг бы ее (хотя некоторые пытаются).
Поэтому можно было бы подумать, что математическое царство — это то место, где выдают «окончательную бумажку» об истине в последней инстанции («фактическую, настоящую бумажку, которая как броня»).
Можно было бы — если бы не Курт Гедель и две его теоремы о неполноте (в одном из материалов на «Горьком» они уже упоминались).
Именитый австриец доказал в начале 1930-х, что всякая достаточно сложная математическая система (а говоря шире — и всякая формальная система) не может одновременно быть полной и непротиворечивой. И что в рамках всякой аксиоматической системы можно сформулировать такое утверждение, которое нельзя ни доказать, ни опровергнуть средствами этой системы.
«Полная система — это такая, в которой все, что в нее входит, можно доказать или опровергнуть. Непротиворечивая — значит не содержащая таких утверждений, которые могут быть одновременно и доказаны, и опровергнуты. Как гром среди ясного неба, теоремы Геделя о неполноте показывали, что в любой математической системе (за исключением самых простых) всегда найдутся утверждения истинные, но недоказуемые. Теоремы о неполноте в каком-то смысле аналогичны принципу неопределенности в физике, поскольку также указывают на существование фундаментального предела познания. И, как и принцип неопределенности, они раздражают и подавляют нас, дразня тем, что реальность — в том числе чисто интеллектуальная — <...> препятствует полному познанию того, что мы пытаемся постичь разумом. Грубо говоря, они показывают, что истина сильнее доказательства — а это ненавистно, особенно для математика».
Авторы «Этой странной математики...» называют теоремы Геделя «сенсационными, шокирующими» и сравнивают с «единственным неизбежным и досадным облаком, омрачающим в остальном ясный горизонт математики».
Давайте немного поразглядываем это небо в алмазах — и начнем с подсчета звезд во Вселенной.
Титаны и мелочь пузатая
Считается, что словом «гугол» в 1920 году Милтон Сиротта — племянник американского математика Эдварда Казнера — обозвал единицу со ста нулями. Вот полная запись числа гугол:
10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
Примерно тогда же появился и «гуголплекс» — число, охарактеризованное девятилетним Сироттой (он потом вырос и тоже стал математиком) как «единица со шлейфом из стольких нулей, сколько сможешь написать, пока не устанешь».
Позже Эдвард Казнер в своей книге «Математика и воображение», написанной в соавторстве с Джеймсом Ньюменом, рассказал широкой общественности о гуголе и гуголплексе, описав последний без опоры на метафору «от забора и до обеда, который никогда не наступит», но более точно — как единица с гуголом нулей:
10гугол
«На всей планете не хватит бумаги, да что там бумаги на Земле — во всей видимой Вселенной не хватит вещества, чтобы записать все знаки гуголплекса, даже если изображать нули размером с протоны или электроны».
Казалось бы, на том бы и успокоиться, но уже в 1933 году математик из ЮАР Стэнли Скьюз получил еще большее число — число Скьюза. Вот оно как выглядит:
1010^10^34
или так еще:
1010^8852142197543270606106100452735038,55
Для сравнения: септиллион — это триллион триллионов, или 1024.
Прошло лет двадцать, и Скьюз объявил, что рассчитал еще большее число. Оно выглядит примерно так (плюс/минус несколько триллионов):
1010^10^964
Параллельно с этим французский математик и физик-теоретик Анри Пуанкаре пытался узнать, сколько времени нужно физической системе, чтобы она вернулась в свое исходное состояние — чтобы вещество и энергия, пройдя через невообразимое количество преобразований и перипетий, перераспределились так, чтобы в точности повторить то, с чего все начиналось (вплоть до субатомного уровня). Это так называемое время возвращения Пуанкаре. Позже канадец Дон Пейдж (аспирант Стивена Хокинга) рассчитает его (время возвращения Пуанкаре) применительно к нашей маленькой уютной Вселенной. Оно описывается числом, которое побольше гуглоплекса и пребывает в рядах титанов где-то между первым и вторым числом Скьюза:
1010^10^10^2,08 лет
Пейдж также рассчитал максимальное время возвращения для любой вселенной определенного типа (не только нашей) — оно еще внушительнее:
1010^10^10^10^1,1 лет
Это уже больше второго числа Скьюза (Пейдж, кстати, представил и физическую аналогию гуголплекса: это число примерно равно количеству микросостояний в черной дыре, сравнимой по массе с галактикой Андромеды — и всем все сразу стало понятно про дыры, гуголплекс и Андромеду).
Пока нас еще не закрутило в водоворот чисел, чью величину даже непонятно с чем сравнивать, вспомним напоследок, что миллионы, биллионы, триллионы и прочую мелочь пузатую описал еще в XV веке французский математик Никола Шюке в своем трактате Le Triparty en la Science des Nombres («Наука о числах в трех частях») — он разбил числа, которые казались тогда непомерно большими (хо-хо), на группы по шесть знаков, назвав их «миллион», «биллион» (вторая отметка), «триллион» (третья) и далее соответственно, вплоть до девятой отметки: «квадриллион», «квииллион», «сикслион», «септиллион», «оттиллион», «нониллион».
Что за зверь на букву «G»
В 1977 году американский математик Рональд Грэм показал всем, что такое настоящая гигантомания. В 1980 году число Грэма занесли в «Книгу рекордов Гиннесса» как самое большое когда-либо использованное в математическом доказательстве. Оно записывается так:
g64
или просто
G
Запись — элегантнее некуда. Однако чтобы приблизиться к этому монстру, нужно разуметь особую запись больших чисел, предложенную американским ученым Дональдом Кнутом, — стрелочную нотацию. Она основана на том, что умножение всегда можно представить как многократное сложение, а возведение в степень — как многократное умножение. 3×4 — то же самое, что 3+3+3+3, а 34 = 3×3×3×3. В нотации Кнута возведение в степень обозначается одиночной стрелкой, направленной вверх: три в кубе (33) записывается как 3↑3, а гугол (он же 10100) — как 10↑100. Повторное возведение в степень записывается так: 3↑↑3 = 33^3. Это операция называется тетрацией («тетра-» — четыре и «итерация» — повторение) — четвертая после сложения, умножения и возведения в степень операция.
Каждая операция является итерацией предыдущей
Благодаря стрелочной нотации Кнута можно добиться компактной записи весьма немалых чисел: 3↑↑3 = 33^3 = 327 = 7 625 597 484 987 (7,6 триллиона с копейками).
Результат математического действия с каждым добавлением стрелок в определенном смысле посильнее «Фауста» Гёте. Потому что результат тетрации числа 4: 4↑↑4 = 4↑4↑4↑4 = 4↑4↑256, что приблизительно равно 10↑10↑154, а это уже больше гуголплекса (10↑10↑100) — того самого, для которого не хватит бумаги и всех веществ.
Раз пошла такая пьянка, то что же останавливаться? Повторная тетрация называется пентацией. И она способна, например, породить число «тритри», записываемое как 3↑↑↑3 (или 3↑↑↑3↑↑↑3, или 3↑↑7 625 597 484 987). Если башни в четыре этажа (немилосердная форма записи) оказалось достаточно, чтобы нагородить число, превышающее гуголплекс, то запись тритри в виде степенной (от слова «степень») башни — это 7 625 597 484 987 троек.
И это только подножие числа Грэма, отделяющее склон от окружающего его рельефа. Добавляем еще стрелку — 3↑↑↑↑3 = 3↑↑↑3↑↑↑3 = 3↑↑↑тритри — получаем:
«В нагромождении степенных башен самая первая у нас 3; вторая — 3↑3↑3, или 7 625 597 484 987; третья — 3↑3↑3↑3...↑3 c 7 625 597 484 987 тройками, то есть тритри; четвертая — 3↑3↑3↑3...↑3, где тритри троек; и так далее. 3↑↑↑↑3 — это башня под номером тритри. Добавив к трем стрелкам еще одну, мы шагнули на гигантское расстояние, так далеко, что уму непостижимо. А пришли всего лишь к g1 — самому первому из серии чисел g, необходимых для того, чтобы добраться до вершины, то есть до самого числа Грэма. <...> Число g2 — это 3↑↑↑↑...↑3 с количеством стрелок, равным g1. Даже робкая попытка осмыслить его масштаб, понять, насколько грандиозными могут быть числа, вызывает головокружение. Всего одна дополнительная стрелка увеличивает результат на феноменальную величину, а в числе g2 таких стрелок g1. В числе g3, как вы уже наверняка догадались, g2 стрелок, в числе g4 — g3 стрелок и так далее. А само число Грэма, G, — это g64».
Мохнатая лапа из вселенной куч
Математическая проблема, которую пытался решить Грэм, попутно создав монстра по имени G, связана с многомерными кубами (n-мерными гиперкубами). Допустим, все вершины такого куба попарно соединены друг с другом отрезками, окрашенными либо в красный, либо в синий. Грэм задался вопросом: каково наименьшее значение n, при котором для любого варианта окрашивания найдутся четыре вершины, лежащие в одной плоскости и попарно соединенные отрезками одного цвета? Ему удалось доказать, что нижний предел для числа n — 6, а верхний — g64.
Так что, пусть это чем-то и похоже на спорт, а чем-то на казино, но меряющиеся самыми большими числами математики занимаются этим не только потому, что это красиво: они решают практические задачи. Это спортивное направление называется «гугология» — в этом клубе занимаются расширением принципиальных возможностей создания все более и более больших чисел.
Например, записать число, превышающее число Грэма, в наше время может почти кто угодно — просто доведя стрелочную нотацию до предела ее возможностей, получив «число Грэма в степени, равной числу Грэма» — g64↑↑↑↑...↑g64 с числом стрелок, равным g64 (то есть примерно g65).
Но лучше не надо. Такое хождение по проторенным дорожкам гугологи не жалуют и называют, как пишут авторы книги, салатом (а по-нашему — шляпой). Нужно создавать принципиально новые системы, которые стали бы инструментарием для еще большего расширения масштабов — да так, чтобы и число Грэма показалось бы уже не таким невозможно невозможным. Проводится и соответствующий конкурс — Big Number Due («Дуэль больших чисел»). Это такой армрестлинг для гугологов.
Бесконечно масштабируемая система в математике существует, она называется быстрорастущая иерархия. Сказав об этом, мы, пожалуй, тут же и замолчим, поскольку если не интернет, то читательское внимание уж точно нерезиновое. Упомянем еще только число Райо (оно больше числа Грэма и его, если не ошибаемся, даже и рассчитать невозможно, но оно есть — и на актуальное время является легитимным чемпионом соревнований по гигантомании). А также о числе BIG FOOT, о котором впервые заговорили в 2014 году (по ссылке на картинке — бигфут, он же сасквоч, «снежный человек» из западной Канады; это его «широкая лапа» вдохновила математиков на создание языка FOOT).
«Чтобы получить хотя бы смутное представление о BIG FOOT, нам придется погрузиться в странную область под названием „вселенная куч” (oodleverse) и выучить язык теории куч первого порядка <...> Да и в любом случае все самые большие на сегодня числа построены по тому же принципу, что и число Райо».
Считаем также должным добавить, что самого большого простого числа не существует — это доказал еще Евклид. Количество простых чисел бесконечно.
На момент написания «Странной математики...» самым большим известным простым числом было 274207281-1, состоящее из 22 338 618 знаков (его вычислил профессор Университета Миссури в Уорренсберге Кертис Купер). Но потом этот рекорд обновился: в декабре 2018 года программа Great Internet Mersenne Prime Search (GIMPS), загруженная в компьютер Патрика Лароша, изловила нового рекордсмена — число 282,589,933 − 1, записывающегося с помощью 24 862 048 цифр. У числа есть и имя — M82589933.
«Настоящее, математическое отверстие»
Еще один «резиновый» раздел математики — топология, где изучают свойства пространств, остающихся неизменными при непрерывных деформациях (то есть, когда форма объекта меняется, но при этом сам он не разрезается и в нем не проделываются новые отверстия).
В этом свете между кружкой с ручкой и «бубликом» (который в топологии называется тор) разницы не то чтобы нет, но она несущественна. В топологии кружка и тор эквивалентны (гомеоморфны), поскольку из первого путем постепенной деформации можно получить второе — ручка чашки превращается в отверстие тора, а самой чашке придается форма кольца вокруг отверстия.
Словом «отверстие» в данном случае называют пронизывающую дыру с двумя концами (просверленные дрелью стены не годятся, поскольку их можно постепенно деформировать так, что они сгладятся, — только саморезы уберите).
А человек, например, гомеоморфен спиннеру. С этой точки зрения уши и половые органы — это скорее впадины, потому что не сквозные и заканчиваются тупиками. Оставшиеся отверстия (вход/выход ЖКТ и ноздри) совмещаются, и мы видим на картине, что человек путем нехитрых манипуляций превращается в тройной тор — спиннер.
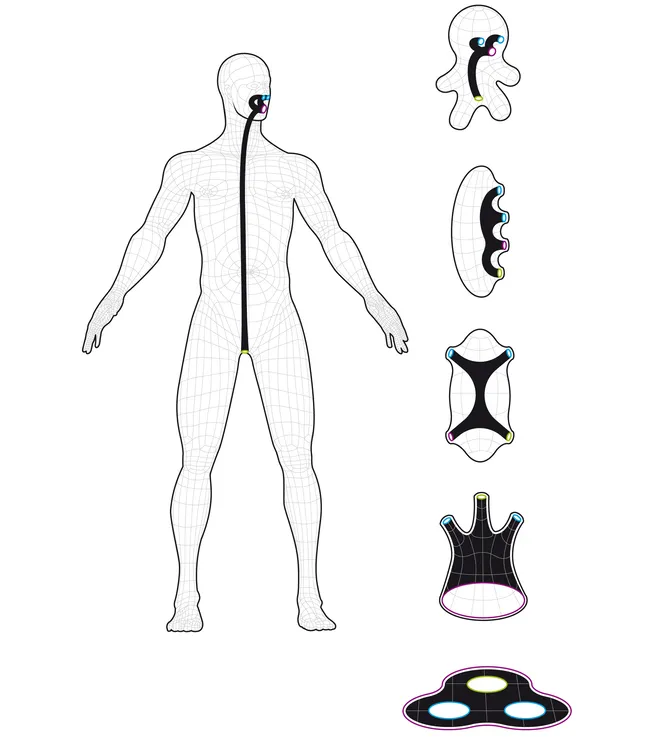
Такое категорически нельзя проделывать тем, у кого в ушах тоннели — дырок больше, поэтому связность будет другой (к слову, количество отверстий в объекте называется родом его поверхности; сфера и куб имеют род 0, тор — род 1, двойной тор («крендель» с двумя дырками) — род 2 и т. д.).
Еще одна весьма неочевидная вещь. Авторы «Странной математики...» пишут о старинной игре «Астероиды», которая жила еще в игровых автоматах. Так вот, из человеческой перспективы все в игре вроде бы происходит на плоском экране, то есть можно было бы подумать, что в двухмерном пространстве. Но самим обитателям аркады их мир представляется в виде тора — они буквально живут на «бублике». Их мир и «бублик» топологически идентичны — и то, и другое тороидальной формы.
«И сферы, и торы, и ленты Мебиуса — все это примеры двумерных поверхностей, которые можно „вложить” в трехмерное пространство. У термина „вложение” есть строгое математическое определение, но, если по-простому, это все равно что поместить одно пространство внутрь другого, отличного от него.<...> это все абстракции, свойства которых никак не зависят от пространства, в котором они находятся: от того, сколько в нем измерений, плоское оно или искривленное и так далее. Но кое-что при вложении в разные пространства все же меняется. Например, тор можно вложить в три измерения (именно в таком виде мы с ним обычно и сталкиваемся), и тогда у него появляются отверстие — настоящее, математическое отверстие — и внешняя и внутренняя стороны. <...> Отверстие — это признак, появляющийся в результате погружения тора в три измерения, а вовсе не постоянное свойство всех торов. В „Астероидах” тороидальная топология пространства проявляется не в отверстии, а в том, как объекты, исчезающие с одной стороны экрана, тут же появляются с другой».
Точно в таком же мире, как и обитатели «Астероидов», живет, например, более антропоморфный, а потому и более близкий нам Pac-Man.
Еще Лейбниц поднял вопрос о разделении геометрии на geometria situs (геометрию положения) и analysis situs (анализ положения). Первая геометрия, о которой рассказывают в школе, — это про вполне приличные фигуры, углы, длины и т. д., тогда как вторая — это геометрия 18+, топологическая камасутра.
Квадрат, например, можно превратить в треугольник (растяжением или сжатием) — и с точки зрения топологии он останется самим собой, разве что поуже в плечах.
И квадрат, и треугольник — идентичны кругу (который можно было бы обозвать «заполненной» окружностью, хотя круг и окружность — это совсем не одно и то же; окружность одномерна — это линия, состоящая из точек, равноудаленных от центра и больше ничего; а у круга есть «внутреннее содержание»). А в трех измерениях куб гомеоморфен шару («заполненной» окружности, хотя двумерная сфера и шар — разные объекты).
В общем, все на самом деле не то, чем кажется. Карл Маркс и Фридрих Энгельс — это не муж и жена, а четыре совершенно разных человека.
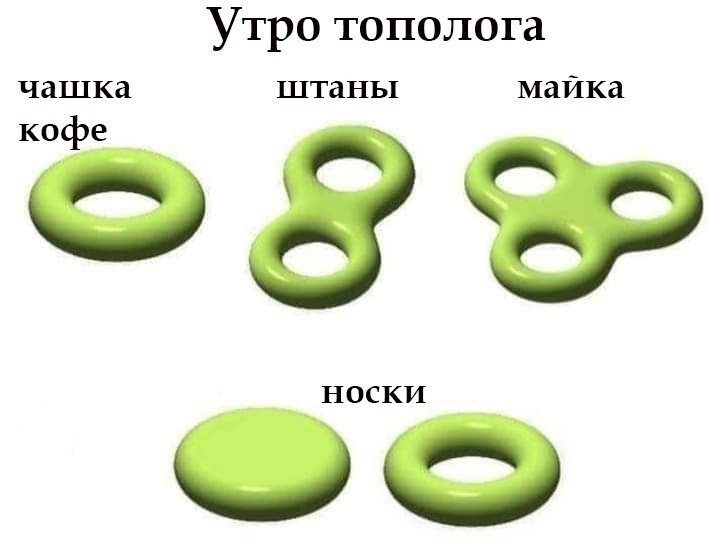Носки тополога такие, потому что в одном из них дырка
Множеством ответвлений своих
Теперь немного поговорим о фракталах. «Чтобы заслужить звание фрактала, фигуре нужно <...> иметь сложную структуру в любом масштабе, сколь бы крупным он ни был». И структура должна быть сложной во всех точках.
Большинство кривых и геометрических фигур не фракталы. Окружность нельзя считать фракталом потому, что, если постепенно увеличивать часть составляющей ее кривой, она будет все больше и больше походить на прямую линию — и более ничего там не увидишь. И квадрат не фрактал, потому что при увеличении его углы не меняют структуру, а все остальное выглядит тоже как прямые линии. И сфера, и куб не фракталы.
Авторы книги приводят метафору береговой линии. Вопросом, как можно в точности измерить ее длину, в начале 1960-х задавался математик и физик Льюис Фрай Ричардсон. Он сделал вывод, что береговая линия не имеет строго определенной длины, а измеренная длина может увеличиваться неограниченно — в том смысле, что она не будет сводиться к какому-то постоянному значению. Так, протяженность испанско-португальской границы по данным испанцев составляла 987 км, а по данным португальцев — 1 214 км.
На географической карте береговой линии мы видим изображение заливов, лагун и полуостровов. Если выйдем на пляж — увидим бухты и косы. Возьмем лупу или микроскоп — познакомимся в подробностях с неровностями валунов и гальки. Уже на этом уровне нет стабильности, потому что результат измерений будет меняться ежеминутно — хотя бы из-за эрозии, приливов и отливов. А на уровень атомов и молекул лучше вообще не соваться.
Этот непроясненный берег — аналог фракталов. Слово это придумал французско-американский математик польского происхождения Бенуа Мандельброт. Фрактал — это нечто (например, кривая или пространство), имеющее дробную размерность.
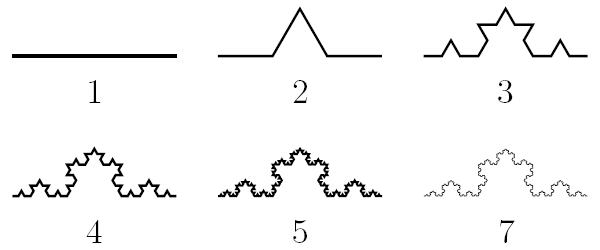
Есть простые фракталы, такие как снежинка Коха или салфетка Серпинского. Делим отрезок прямой на три равные части, затем используем среднюю в качестве основания и строим на ней равносторонний треугольник, а потом его основание стираем. Повторяем процесс на каждом из получившихся четырех коротких отрезков, затем — на каждом из новых очень коротеньких отрезков и так далее.
А вот визуализация множества Мандельброта — единого фрактала, содержащего в себе бесконечное число совершенно непохожих друг на друга фракталов (все ответвления не копии, среди них нет двух абсолютно идентичных) в виде гигантского массива множеств Жюлиа, расположенных вдоль его границы.
«В основе любого природного явления, которое кажется нам случайным и неупорядоченным, может лежать фрактал. Более того, можно даже утверждать, что все объекты и явления, существующие в этом мире, — фракталы, поскольку все они на любом уровне имеют ту или иную структуру, по крайней мере до уровня атомов. Облака, вены на руке, разветвления бронхов, листья деревьев — все они имеют структуру фрактала. В космологии по фрактальному принципу распределяется материя по Вселенной, и фрактал этот имеет структуру даже на уровнях меньше атомного ядра, вплоть до предельного значения расстояния, которому присвоен физический смысл, — так называемой планковской длины <...> или приблизительно одной стоквинтиллионной размера протона».
Дудл Google к 111-летию Гастона Жюлиа
«Яркий пример — человеческое легкое. Поскольку само легкое очевидно трехмерно, его поверхность, по идее, должна быть двумерной. Однако в процессе эволюции легкое обрело огромную площадь поверхности — около 80–100 квадратных метров, в половину теннисного корта, — чтобы максимально ускорить газообмен».
***
Такой математикой не заинтересоваться, пожалуй, нельзя. Ее, правда, легко не понять, но уж точно невозможно забыть.