База орнамента

Все мы начиная с 24 февраля 2022 года оказались перед лицом наступающего варварства, насилия и лжи. В этой ситуации чрезвычайно важно сохранить хотя бы остатки культуры и поддержать ценности гуманизма — в том числе ради будущего России. Поэтому редакция «Горького» продолжит говорить о книгах, напоминая нашим читателям, что в мире остается место мысли и вымыслу.

Никос Салингарос. Теория архитектуры. М., Екатеринбург: Кабинетный ученый, 2025. Перевод с английского Ирины Бембель и Татьяны Быстровой. Содержание

Наука о паттернах

Математика определяет отношения и паттерны. Разум воспринимает связи и взаимосвязи между понятиями и идеями, затем связывает их воедино. Способность создавать паттерны является следствием развития нашей нервной системы, реагирующей на среду. Математические теории объясняют отношения между паттернами, возникающими в упорядоченных, логичных структурах. Паттерны разума подражают паттернам в природе, а также паттернам, созданным человеком, и, вероятно, именно так развивался человек, чтобы стать способным к математике. Только интеллект, превышающий определенный порог развития, способен распознавать паттерны. Человечество генерирует паттерны из какой-то базовой внутренней потребности: паттерны воплощают в себе связные структуры, сформированные в процессе мышления, что объясняет повсеместное распространение визуальных паттернов в традиционном искусстве и архитектуре.

Временны́е паттерны тоже необходимы для интеллектуального развития человека. Повседневная деятельность организуется в соответствии с природными ритмами. Ежегодно происходящие события становятся точками, которые фиксирует социум. Более того, они часто связывают общество с научным пониманием периодических природных явлений, таких как времена года и их следствия. Сама математика возникла из необходимости вести летопись наблюдаемых закономерностей в пространстве и времени. Все известные мифы, объясняющие происхождение мира, в значительной степени опираются на паттерны, указывая на рождение мира как на формирование закономерности из случайности. Повторяющиеся в малых масштабах жесты и движения становятся театром и танцем, включаются в миф, ритуал и религию. Развитие голоса и музыки отвечает потребности в организации и кодировании ритмических паттернов и сообщений. Все эти виды деятельности наблюдаются в виде паттернов в жизненном цикле человека.

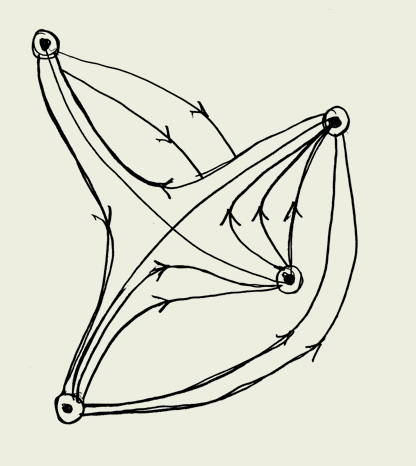
Известно, что в результате самоорганизации сложные физические и химические системы генерируют паттерны в пространстве или времени. Организованная сложность системы проявляется в виде воспринимаемых паттернов в макроскопическом масштабе. Это относится не только к встречающимся в природе бесчисленным статичным паттернам; паттерны представляют собой коллективные движения или другие формы организованного поведения (примерами могут служить конвективные ячейки, океанические течения и водовороты в реках). Наблюдение устойчивых паттернов в динамических системах часто свидетельствует о том, что диссипативная система — наиболее оптимальное для передачи энергии состояние (например, в водовороте выгоднее избавиться от избытка энергии, чем при беспорядочном движении, что является причиной возникновения ураганов). Напротив, в однородном состоянии мало что происходит упорядоченно.

До эпохи массового образования, а многим людям и сегодня, архитектурные паттерны дают один из немногих первичных контактов с математикой. Черепица крыш и орнамент стен являются «видимой вершиной» математики, для понимания и оценки которой в других случаях требуется изучение специального языка. Тысячи лет для огромной части населения Земли геометрические паттерны архитектурной среды были единственным источником математического образования. Теперь всего этого уже нет. Я считаю, что подсознательное усвоение математической информации помогало людям лучше справляться со сложностями жизни и среды. В паттернах проявляются врожденные творческие способности и талант к математике, которыми обладают все. Детские психологи признают инструментальную значимость паттернов в визуальной среде развивающегося ребенка.

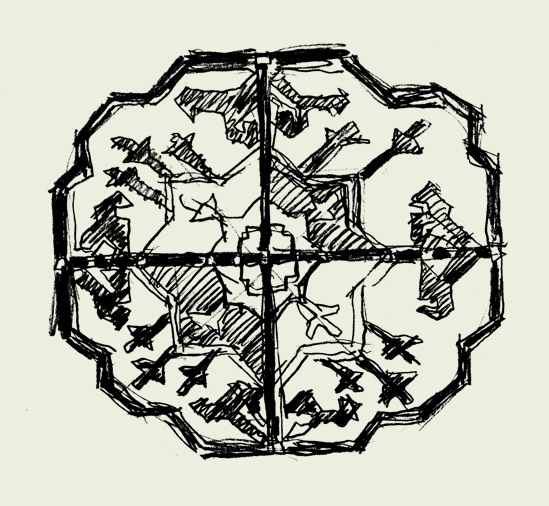
Как один из характерных образцов традиционной материальной культуры, восточные ковры представляют особый вид создания и воспроизведения визуальных паттернов, существующий уже несколько тысячелетий. Ковры — это микрокосм мировоззрения и идентичности, записанный посредством текстиля и природных красителей и передаваемый из поколения в поколение через традицию ткачества. Существует тесная связь между дизайном ковров и математическими правилами организации сложности. Второй пример — напольные покрытия в западной архитектуре, которые сегодня рассматриваются как хранилище математической информации.

Паттерны Александера как унаследованные архитектурные решения

Попытка определить паттерны в области проектирования предпринята Кристофером Александером и его коллегами в ходе сбора повторяющихся архитектурных и городских решений в книге «Язык шаблонов». Когда похожие решения возникают независимо друг от друга в разное время и в разных культурах, они, очевидно, воплощают один или несколько инвариантов. «Паттерны» Александера выводят вечные архетипы, такие как: необходимость света с двух сторон комнаты, хорошо продуманный вход, взаимодействие пешеходных и автомобильных дорог, иерархия приватности в разных комнатах дома и т. д. Ценность «Языка шаблонов» Александера заключается в том, что эта работа не о конкретных типах зданий, а об архитектурных архетипах. Каждый из них представляет собой проверенное решение (т. е. паттерн), и эти решения можно комбинировать бесконечным количеством способов. Это подразумевает более математический, комбинаторный подход к проекту в целом.

У Александера паттерны — это решения, повторяющиеся во времени и пространстве, поэтому они сродни визуальным паттернам, перенесенным в другие, абстрактные измерения. Каждая серьезная наука собирает обнаруженные закономерности в корпус решений, составляющий ее основу. Наука (и следом за ней человечество) развивалась путем каталогизации закономерностей, наблюдаемых в природных процессах, для создания различных предметов упорядоченного знания.

Однако не следует путать паттерны Александера с сугубо визуальными паттернами. Паттерн/решение связывает как социальные, так и геометрические компоненты, способы использования и практики. Чисто визуальный паттерн может быть привлекательным, но не иметь отношения к конкретным человеческим потребностям и деятельности. Те, кто проектирует с сугубо визуальной точки зрения, не могут оценить всю важность паттернов Александера. Тем не менее визуальные паттерны и паттерны Александера имеют общую концептуальную основу. Как показано далее, исключение визуальных паттернов из среды дает образ мышления, который ценит только уникальные, невоспроизводимые случаи; его следствие — устранение всех паттернов, как визуальных, так и связанных с практическими решениями. К счастью, конкретные структурные решения (тоже паттерны), от которых зависят архитекторы, остаются частью инженерного дела, где, в отличие от архитектуры, накопленные знания сохраняются для повторного использования.

Основные законы проектирования гармоничных зданий представлены в более поздней работе Александера. Удачные здания — те, что адаптируются к человеческим потребностям и чувствам и подчиняются тем же системным законам, что сложный организм или эффективная компьютерная программа. Такие теоретические результаты в конечном итоге станут частью основного корпуса архитектурных знаний. Можно игнорировать потребность в повторно используемых архитектурных решениях, но невозможно ее обойти. Если архитектурная наука не обеспечивает ими (давая нам визуальные паттерны, а не адаптивные решения), то кто-то другой придумает, возможно, менее эффективные заменители решений. Проектирование обычных зданий уже берут на себя сами жители при строительстве жилых домов или подрядчики — при возведении коммерческих зданий. Строители разработали собственный набор (обычно очень плохо адаптированных) архитектурных моделей, обусловленных желанием минимизировать затраты и стандартизировать компоненты, а не оптимизировать адаптацию к человеку или связь с ним. Архитекторы все чаще проектируют только здания-«витрины», о которых пишут в архитектурных журналах, но которые составляют все меньший процент от того, что реально строится сегодня.

Архитектурное образование, как правило, сосредоточено на попытках развить «креативность». Классические паттерны симметрии и упорядоченности отвергаются как устаревшие и неподходящие для прогресса архитектуры. Студента побуждают изобретать новые решения, игнорируя полезный опыт прошлого, но не учат, как оценить, хороши или плохи эти решения. Такой подход игнорирует повторяющиеся паттерны, которые могут быть найдены в пространстве всех возможных проектных решений. Современная архитектура оценивает проекты только по тому, насколько они соответствуют какому-то субъективному мнению об инновациях. Единственный способ избежать возвращения к традиционным архитектурным паттернам, которые настолько хорошо работают на практике, что их постоянно открывают заново, — это блокировать дедуктивный процесс, связывающий следствие с его причиной. Намеренное пренебрежение причинно-следственной связью при проектных решениях приводит к тому, что архитектурные и градостроительные ошибки повторяются снова и снова, каждый раз приводя к одним и тем же катастрофическим последствиям.

Математика и архитектура

Исторически архитектура была частью математики, и в прошлом эти две дисциплины часто не различались. В древнем мире математики были архитекторами, чьими сооружениями — пирамидами, зиккуратами, храмами, стадионами и оросительными системами — мы восхищаемся сегодня. В классической Греции и Древнем Риме от архитекторов требовалось быть еще и математиками. Когда византийскому императору Юстиниану понадобился архитектор для строительства храма Святой Софии как здания, которое превзойдет все, построенное до него, он обратился за помощью к двум знатокам математики (геометрам), Исидору и Анфимию. Эта традиция продолжилась в исламской цивилизации. Вклад исламского мира в мировую математику начался, когда математическая мысль помогала создавать его самые запоминающиеся здания. Исламские архитекторы создали множество двухмерных паттернов на керамической плитке на века раньше, чем западные математики дали их полную классификацию.

Средневековые каменщики хорошо разбирались в геометрии, что позволило им возводить великие соборы в соответствии с математическими принципами. Они использовали экспериментальный метод для разработки новых типов объектов. Не совсем справедливо называть средневековье периодом без математики: его математика встроена в здания, а не записана. Прискорбная потеря грамотности на Западе в течение этих веков совершенно точно не сопровождалась потерей визуальных или архитектурных паттернов в таких же масштабах, потому что паттерны (в отличие от абстрактных правил письменности) отражают процессы в разуме. В любой традиционной архитектуре есть математика.

Меня интересует здесь то, что произошло в XX веке. В 1908 году австрийский архитектор Адольф Лоос запретил орнамент в архитектуре абсурдными и ничем не подкрепленными заявлениями:

«Эволюция культуры синонимична удалению орнамента с утилитарных объектов. <...> Орнамент не только производится преступниками, само преступление состоит в том, что орнамент наносит серьезный ущерб здоровью людей, государственному бюджету и, следовательно, культурной эволюции. <...> Свобода от орнамента — признак духовной силы».

Эти враждебные, расистские настроения разделял швейцарский архитектор Ле Корбюзье:

«Декорирование, как и цвет, — явления чувственного, примитивного порядка, которые подходят простым расам, крестьянам и дикарям. <...> Крестьянин любит орнамент и украшает свои стены».

Два этих архитектора осудили материальную культуру всего человечества, накопленную за тысячи лет (и другие архитекторы им безоговорочно поверили). Хотя это может казаться действием, представляющим чисто стилистический интерес, на деле оно имеет серьезные косвенные последствия. Удаление орнамента устраняет все упорядоченные структурные различия из диапазона масштабов от 5 мм до 2 м или около того, что соответствует объектам человеческого масштаба, т. е. размерам глаза, пальца, кисти, руки, тела и т. д. По канонам модернистского дизайна, детали в таких масштабах не могут быть определены, и это удаляет из архитектурной среды математическую информацию. Глядя на здания XX века, трудно обнаружить визуальные паттерны в любом из нескольких различных масштабов. Действительно, архитекторы прилагают большие усилия, чтобы замаскировать сомасштабные человеку паттерны, которые обусловлены происходящими в здании процессами; как и те, которые возникают в материалах как следствие конструктивных особенностей и эрозии.

Когда визуальные паттерны воспринимаются непосредственно, они оказывают наиболее сильное эмоциональное и когнитивное воздействие. Имеет смысл различать абстрактные паттерны на плане здания и воспринимаемые паттерны на фасадах, стенах, крышах здания или на мостовых. Только вторые оказывают непосредственное влияние на человека, потому что они видны и ощущаются мгновенно. В последние несколько десятилетий архитекторы и урбанисты одержимы идеей навязывания плану здания непродуманных паттернов и симметрий. Из-за перспективы, занимаемой позиции и роста человека они не всегда заметны, даже если объект — это открытая площадь. В обычном здании, обнесенном стеной, паттерны его плана по большей части скрыты от глаз. Пользователю приходится мысленно восстанавливать план здания, т. е. план воспринимается разумом и только через некоторые усилия. Это согласуется с формальным подходом к проектированию, когда смысл, значимый для наших перцептивных способностей, пытаются заменить на смысл, значимый для способностей интеллектуальных.

Пропорциональные соотношения можно включить в качества архитектуры, воспринимаемые только косвенно. Золотое сечение Φ ≈ 1,618, соотношения 5 : 3, 8 : 5 встречаются в архитектуре повсеместно, и эта тема дает богатое поле для изучения. Тем не менее никакая конкретная математическая информация не сообщается людям, пользующимся комнатой или фасадом с необходимыми общими пропорциями, и этот эффект играет лишь вторичную эстетическую роль. В действительности использование пропорциональных соотношений в рамках традиционного канона проектирования подразделяет формы так, чтобы определить совпадающие масштабы (т. е. субъединицы в иерархии масштабов), создавая иерархическую согласованность, дающую значимый позитивный эффект.