Хаим Шапира. Восемь этюдов о бесконечности. Математическое приключение. М.: КоЛибри, Азбука-Аттикус, 2021. Перевод с английского Дмитрия Прокофьева. Содержание
Бесконечность — это иррационально
Удивительно, но человечество далеко не сразу пришло к пониманию иррациональной сути бесконечности. Мы привыкли, что рациональность — это наивысшая степень ясности и логичности, нечто, присущее прежде всего строго разработанной науке, однако первобытные мифы обладали не менее четкой логикой. Понадобился гений древних греков, чтобы нехотя, со скандалом, но признать не укладывающуюся ни в какую логику бесконечность. Считается, что первым ее ввел в философский обиход Анаксимандр, автор концепции апейрона, хотя апейрон у него обозначал скорее неопределенность. Такая бесконечность особых возражений еще не вызвала. А вот Пифагору открылось нечто совершенно возмутительное. Пифагор-философ считал, что все состоит из натуральных (то есть положительных целых) чисел и ими может быть выражено. Числа были атомами его мира. А Пифагор-математик обнаружил, что соотношение между стороной квадрата и его диагональю невозможно выразить отношением натуральных чисел. Иными словами, √2 — иррациональное число (напомним: иррациональность числа подразумевает, что, во-первых, его десятичное представление бесконечно, а во-вторых, в нем никогда не возникают какие бы то ни было повторяющиеся структуры).
Джин из бутылки был выпущен. Две тысячи лет спустя Георг Кантор показал, что «почти» все вещественные (или действительные) числа иррациональны. Среди них и два самых важных числа в математике — число Эйлера и отношение длины окружности к ее диаметру, число п.
Кстати, когда в 1593 году французский математик Франсуа Виет нашел замечательную формулу для вычисления π при помощи набора вложенных радикалов, он записал ее в следующем виде:
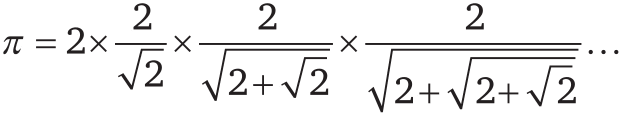Стоящее в конце многоточие означает «продолжать ту же процедуру до бесконечности». Это первый случай, когда бесконечный процесс был явно обозначен в математической формуле. Ну а знаменитый знак бесконечности ∞ впервые использовал английский математик Джон Валлис в 1655 году.
Бесконечность — это парадоксально
Вернемся к грекам. По-настоящему скандал с бесконечностью раздул Зенон Элейский, ученик Парменида. С тех пор его знаменитые апории обсуждались бесчисленное количество раз. Рассел называл их «неизмеримо тонкими и глубокими», а Пуанкаре, напротив, эмоционально заявлял, что «Зенон был идиотом, и только идиоты могут заниматься его апориями».
До нас дошли девять апорий, но наиболее известны из них три. «Стрела» — о стреле, которая в каждый момент времени покоится, а значит, никуда не летит. «Дихотомия», в которой идущий из точки A в точку B никогда туда не доберется, так как ему сначала нужно пройти половину этого расстояния, а затем половину оставшегося расстояния и так далее, так что до точки B всегда будет оставаться еще какая-то крошечная половинка. И, конечно же, «Ахиллес и черепаха» — в которой Ахиллес никогда не догонит черепаху, если та пустилась в путь немного раньше, так как всякий раз, как Ахиллес прибывает на то место, где только что была черепаха, та успевает продвинуться хоть чуть-чуть, но дальше.
Рассуждения Зенона безупречны, однако допустить в реальности, чтобы бегун не перегнал какое-то пресмыкающееся, попросту нелепо. Так была найдена парадоксальная сторона бесконечности, которая противоречит всему нашему опыту. Изящным математическим выражением этой парадоксальности служит простое уравнение 1=0,999999... Здесь всякий поначалу заподозрит какой-то подвох. Нет, тут не может быть знака равенства: пусть на ничтожную величину, но правая часть формулы все-таки должна быть меньше единицы! Однако доказательство элементарно и безжалостно. Пусть a=0,9999999... В таком случае 10a=9,999999... Вычтя одно число из другого, получим 10a — a = 9,999999... — 0,999999... Что дает 9a=9, то есть a=1.
В бесконечности — значит нигде
Еще одна парадоксальная характеристика заключается в том, что, по формулировке Гегеля, «бесконечность нельзя найти ни в одной точке бесконечной прямой». Представим себе космический корабль, который движется по следующим правилам: первые полчаса он летит со скоростью 2 километра в час (или 2 тысячи, или 2 миллиона, что совершенно неважно). На следующую четверть часа его скорость несколько возрастает — до 4 километров в час. В течение следующей одной восьмой часа он летит со скоростью 8 километров в час — и так далее. Где этот космический корабль окажется через час? Цифры подобраны таким образом, чтобы получить несложный расчет: за первые полчаса он пролетит километр, за следующие четверть часа — еще километр, и так далее, то есть в итоге он преодолеет расстояние 1+1+1+1... Но поскольку это число бесконечно, мы не можем указать ни одну точку в космосе, где бы мог оказаться корабль, ведь до любой точки будет пусть сколько угодно большое, но конечное расстояние. Корабль попросту нигде, он исчез из нашего вычислимого мира. Словно бы перешел на иной уровень существования.
Бесконечность — это красиво
Греков бесконечность пугала. Она была чем-то вроде вторжения хаоса в их упорядоченный и размеренный космос. Однако вскоре обнаружилось, что бесконечность обладает своей завораживающей красотой, своей «рациональностью». Эта красота, например, очевидна в приведенной выше формуле Виета для вычисления π. А вот еще одна невероятная красота:
1/9801 = 0,0001020304050607080910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758...
Для наглядности напишем это число с пробелами:
1/9801 = 0,00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 99 00 01 02 03... 97 99 00 01 02 03 04 05 06...
Мы получили все двузначные числа, расположенные в правильном порядке и повторяющиеся до бесконечности, кроме числа 98! По сравнению с подобным меркнет вся красота конечного мира, ведь здесь мы прикасаемся к чему-то запредельному и как бы божественному — к той гармонии, которая, возможно, лежит в основе всего (а теперь попробуйте самостоятельно поделить 1 на 998 001).
Бесконечность — это божественно
В 1913 году профессор математики Кембриджского университета Годфри Харди получил письмо из Индии от никому не известного индийского юноши, закончившего только среднюю школу. В письме было несколько уравнений, потрясших Харди. Например:
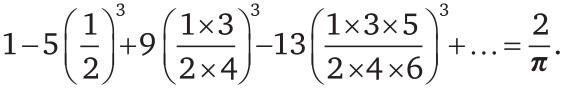Так мир узнал о Рамануджане. Он был гениальным самоучкой и поддерживал с числами какие-то мистические отношения. Иначе невозможно объяснить, как Рамануджан открывал свои формулы.
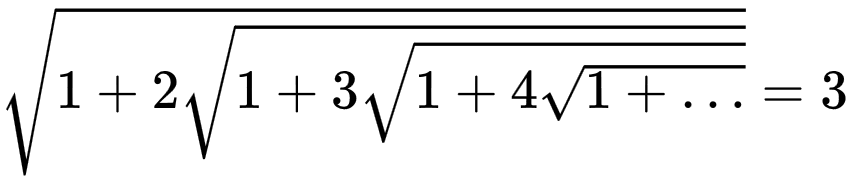Многие сравнивали их с симфониями Моцарта или картинами эпохи Возрождения, но сам Рамануджан утверждал, что они внушались ему во время сна или медитации богиней Махалакшми. Как знать, не боги ли поспешили забрать к себе индийского гения (Рамануджан умер в 32 года), ведь он и так выдал немало их секретов. Подобных формул он успел записать более 3 900!
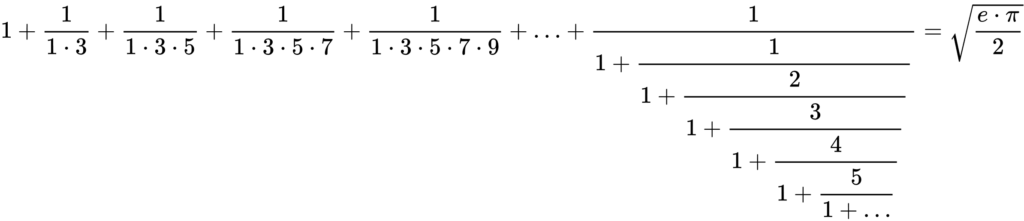
Брадобрей уделывает Кантора
Еще одним человеком, состоявшим с бесконечностью в чрезвычайно близких отношениях, был Георг Кантор, наш соотечественник (он родился в Санкт-Петербурге в 1845 году). Ему принадлежит разработка теории множеств, которая стала прорывом в математике. До него считалось, что «бесконечность распознаваема, но не познаваема» (Декарт). В лучшем случае бесконечность оценивали «на глазок», как, например, Эйлер, полагавший, что бесконечность 2/0 вдвое больше, чем 1/0. Кантор математически показал, что бесконечные множества (как и конечные) можно сравнивать, производить над ними операции, формулировать и доказывать теоремы с ними. Однако и здесь сразу же вмешались парадоксы — куда без них в бесконечности?
Когда Готлоб Фреге уже заканчивал фундаментальный двухтомный труд «Основные законы арифметики», в основу которого были положены выкладки Кантора, он получил письмо от Бертрана Рассела, заставившее его посыпать голову пеплом. В этом письме Рассел вывел свой знаменитый парадокс брадобрея, который бреет всех, кто не бреется сам. За софистическим с виду содержимым скрывалась серьезная проблема.
В теории Кантора множество — это совокупность каких-то объектов. Если среди этих объектов нет самого множества, такое множество считалось обычным. Например, множество всех кроликов само кроликом не является. Но множество не-кроликов уже «необычно» — ведь оно тоже «не-кролик», значит, входит в самого себя. Такое множество стали называть расселовским. Парадокс возникает, когда рассматривается множество всех обычных множеств, которое оказывается не обычным, не расселовским. Оно не обычное, так как, будучи обычным множеством, должно входить в самого себя, то есть на самом деле быть расселовским множеством. И оно не расселовское, так как, если оно входит в самого себя в качестве расселовского, это противоречит его определению как множеству только обычных множеств. Таким образом, оказалось, что разделение множеств на те, что не являются собственными элементами, и те, что являются таковыми, не исчерпывает всех множеств. Есть еще и «брадобреи».
Гранд-отель «Бесконечность» имени Гильберта: свободные номера есть всегда!
Немецкий математик Давид Гильберт придумал, пожалуй, самый изящный пример, связанный с парадоксами бесконечности. Представим себе отель с бесконечным количеством номеров, в котором живут постояльцы — все натуральные числа: 1, 2, 3, 4... Свободных номеров, естественно, нет, что вполне устраивает портье. Но вот в гостиницу пожаловал важный гость: 0. Можно ли его разместить? Сообразительный портье попросил каждого из жильцов переехать в следующий по порядку номер, освободив тем самым для ноля № 1. Лиха беда начало. Стало известно, что в отеле все-таки могут быть свободные номера, и первыми подсуетились все отрицательные числа, которых, понятно, тоже бесконечность. Прежний способ не работает: нельзя попросить постояльцев переехать на бесконечное число номеров. Однако можно переселить каждого жильца в номер с удвоенным значением: 2 в № 4, 3 в № 6 и так далее. Тогда все нечетные номера (3, 5, 7, 9...) освободятся и получится бесконечное количество незанятых комнат.
Слава о гостинице, в которой всегда есть свободные номера, растет, и теперь сюда желают пожаловать все положительные рациональные дроби. Портье с ужасом осознает, что прежний метод опять бесполезен: ведь одни только числа со знаменателем 2 могут полностью занять отель, если дробь ½ поселится в № 1, дробь 2/2 — в № 2, дробь 3/2 — в № 3 и так далее. А таких знаменателей бесконечность! То есть нужно разместить бесконечное количество бесконечных множеств. Тем не менее наш портье блестяще справился с этой задачей, оставив про запас еще одну бесконечность номеров. Как? Прочитайте в книге или посмотрите наглядный ролик.
Гранд-отель «Бесконечность» имени Гильберта: трест, который лопнул
Итак, в гостиницу постоянно и без проблем въезжают разные бесконечности и даже бесконечности бесконечностей. Поэтому портье и глазом не моргнул, когда к стойке регистрации подошло скромное множество всех чисел между 0 и 1. Конечно, в этом интервале тоже содержится бесконечное количество, но разве не в этом специализация нашего отеля? Однако все попытки перемножать, возводить в степень и прочие манипуляции с номерами ни к чему не привели: числа между 0 и 1 в отель не влезали. В отчаянье портье даже выселил всех постояльцев, но и пустая гостиница не могла вместить в себя не то что все числа между 0 и 1, но даже дроби, записанные с использованием только цифр 0 и 1, то есть 0,101 и так далее. Репутация отеля обвалилась, поползли слухи, что гранд-отель «Бесконечность» на самом деле маленький. Торжествующие конкуренты немедленно открыли рядом «Еще большую бесконечность». Но как такое возможно?
«Вижу, но не верю!»
Мы уже упоминали, что именно Кантор научился сравнивать бесконечные множества. Оказалось, что счетные множества (элементы которых можно пронумеровать натуральными числами) — это самые простые или «маленькие» множества. Их мощность (то есть количество элементов) обозначается буквой еврейского алфавита ℵ0 («алеф-нуль»). Мощность несчетных (состоящих из вещественных чисел) множеств больше и обозначается как ℵ. Равна ли она ℵ1, математики спорят до сих пор, однако несомненно, что есть множества с мощностью ℵ2, ℵ3 и так далее.
Мы видели, что даже простые счетные множества очень интересны, так как позволяют включать в себя разные бесконечности. Обладают ли таким свойством несчетные множества? Конечно! Их еще называют континуум-множествами, так как геометрически их можно представить в виде непрерывных отрезков или линий. При этом любые два отрезка равномощны, то есть имеют равное (хоть и несчетное) количество своих точек. Доказательство легко видно из рисунка:
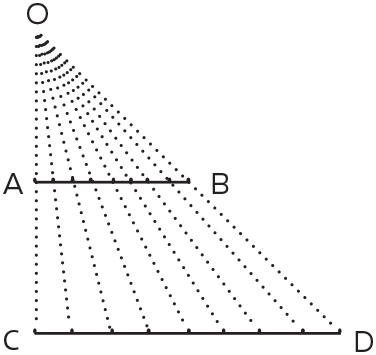С этим еще можно согласиться, но как вам равномощность любого конечного отрезка и бесконечного луча? Однако она становится очевидной, если провести те же линии соответствия на следующем рисунке:
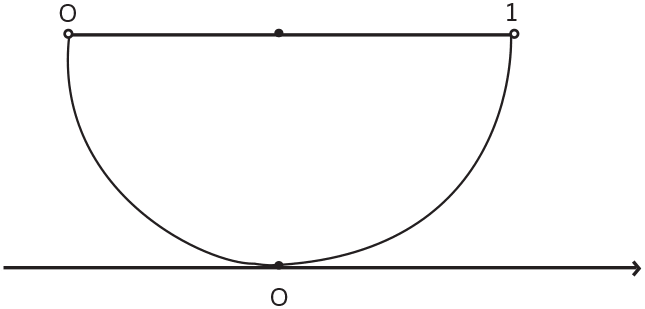И уж совсем невероятна равномощность бесконечной прямой и n-мерного пространства (для любого n!). Говорят, когда Кантор доказал это, он воскликнул: «Je le vois, mais je ne le crois pas!» («Вижу, но не верю!»)
Бесконечность — это трансцендентно
Теория счетных и несчетных множеств позволяет проникнуть в совсем уже запредельную тайну бесконечности. Как мы писали, все действительные числа можно разделить на рациональные и иррациональные. Однако в математике куда важнее другое разделение: на алгебраические и трансцендентные. Число называется алгебраическим, если оно является корнем какого-либо многочлена с целыми коэффициентами (простейший пример: bx — a). Любое рациональное число будет решением подобного многочлена, как и некоторые иррациональные числа: например, √2 является корнем уравнения x2 — 2 = 0. Характеристика алгебраичности очень важна, так как все алгебраические числа образуют счетное множество, внутри которого возможны четыре основных алгебраических действия: сложение, вычитание, умножение, деление (разумеется, кроме деления на 0).
А что же с неалгебраическими числами, то есть теми, которые невозможно представить в виде корней многочленов и которые образуют несчетное множество? Долгое время их попросту не могли найти! И только в 1844 году французский математик Жозеф Лиувилль открыл первое трансцендентное число. Вот оно:
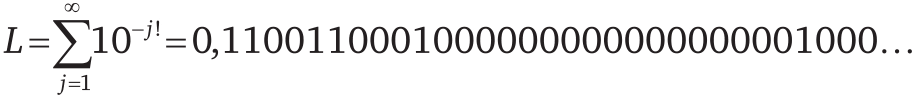Строится оно следующим образом. Сначала вычисляем все факториалы: 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120... Затем составляем число, в котором после запятой встречаются только нули и единицы, причем 1 стоит на 1, 2, 6, 24, 120-м — и так далее — местах, а на всех остальных местах стоит 0. Лиувилль доказал, что это число не является корнем какого бы то ни было алгебраического уравнения с целыми коэффициентами.
Можно подумать, такое число — редкий зверь в числовом зверинце, но ничего подобного! Кантор обнаружил, что трансцендентные числа составляют большинство всех чисел. Другими словами, практически все числа не только не рациональны, по большей части они даже не относятся к алгебраическим!
Но где же тогда все эти трансцендентные числа? Видимо, где и должны быть: в трансцендентной бесконечности. Лишь некоторые нам удается изловить оттуда, изощренно доказывая, что они не являются алгебраическими. Так, трансцендентность числа π была доказана лишь в 1882 году, трансцендентность постоянной Гельфонда eπ — в 1934-м, а десятичный логарифм ln π до сих пор ждет решения своей судьбы. Бесконечность неохотно раскрывает свои тайны, коих у нее, без сомнения, бесконечное множество.